CUSTOM
SOLUTIONS

BACK
PRICES
ORDER
HOME
|

|
|
Mathematica 5.2 Professional Version for Windows
From simple calculator operations to large-scale programming and interactive-document preparation,
Mathematica is the tool of choice at the frontiers of scientific research, in engineering analysis
and modeling, in technical education from high school to graduate school, and wherever quantitative
methods are used.
What Is Mathematica?
You probably know Mathematica by name. Or you may be one of nearly two million users. But do you really
know the breadth of capabilities Mathematica can offer you? Whatever you're working on--calculating,
programming, learning, documenting or developing--Mathematica is equipped to help.
Mathematica seamlessly integrates a numeric and symbolic computational engine, graphics system,
programming language, documentation system, and advanced connectivity to other applications. It is
this range of capabilities--many world-leading in their own right--that makes Mathematica uniquely
capable as a "one-stop shop" for you or your organization's technical work.
Wide Range of Uses
- Handling complex symbolic calculations that often involve hundreds of thousands or millions of terms
- Loading, analyzing, and visualizing data
- Solving equations, differential equations, and minimization problems numerically or symbolically
- Doing numerical modeling and simulations, ranging from simple control systems to galaxy collisions,
financial derivatives, complex biological systems, chemical reactions, environmental impact studies,
and magnetic fields in particle accelerators
- Facilitating rapid application development (RAD) for engineering companies and financial institutions
- Producing professional-quality, interactive technical reports or papers for electronic or print distribution
- Illustrating Mathematical or scientific concepts for students from K-12 to postgraduate levels
- Typesetting technical information--for example, for U.S. patents
- Giving technical presentations and seminars
Works at All Levels
Usually Mathematica is used with its notebook interface directly as it comes out of the box. However,
it is increasingly being used through alternative interfaces such as a web browser or by other systems
as a back-end computational engine.
Some of these uses require in-depth Mathematica knowledge, while others do not. Mathematica is unusual
in being operable for less involved tasks as well as being the tool of choice for leading-edge research,
performing many of the world's most complex computations. It is Mathematica's complete consistency in
design at every stage that gives it this multilevel capability and helps advanced usage evolve naturally.
Fully Featured, Fully Integrated
At a superficial level, Mathematica is an amazing, yet easy-to-use calculator. The world's most
comprehensive set of Mathematical, scientific, engineering, and financial functions is ready-to-use--often
with just one mouse click or command. However, Mathematica functions work for any size or precision
of number, compute with symbols, are easily represented graphically, automatically switch algorithms to
get the best answer, and even check and adjust the accuracy of their own results. This sophistication
means trustworthy answers every time, even for those inexperienced with the mechanics of a particular
calculation.
While working through calculations, a notebook document keeps a complete report: inputs, outputs, and
graphics in an interactive but typeset form. Adding text, headings, formulas from a textbook, or even
interface elements is straightforward, making online slide show, web, XML, or printed presentation
immediately available from the original material. In fact, with notebook document technology, a fully
customized interface can easily be provided so that recipients can interact with the content. The
notebook is a fully featured, fully integrated technical document-creation environment.
Easy Programming, Powerful Results
The move from immediate calculations to programmed computations can occur evolutionarily. Just one
line makes a meaningful program in Mathematica--the methodology, syntax, and documents used for input
and output remaining as they are for immediate calculations.
Mathematica is also a robust software development environment. Mathematica packages can be debugged,
encapsulated, and wrapped in a custom user interface, all from within the Mathematica system.
Alternatively, Java, C, or links to a proprietary system can use Mathematica's power behind the
scenes.
One Unifying Idea
Symbolic programming is the underlying technology that provides Mathematica this unmatched range of
abilities. It enables every type of object and every operation--be they data, functions, graphics,
programs, or even complete documents--to be represented in a single, uniform way as a symbolic
expression. This unification has many practical benefits from ease of learning to broadening the
scope of applicability of each function. The raw algorithmic power of Mathematica is magnified and
its utility extended.
Key Elements of Mathematica
Notebook Document System
Mathematica notebooks provide a complete technical document system with typeset math, sound,
graphics, and animations.
Whether you are creating a report, an academic paper, courseware, or an electronic book or just want to
keep a record of your work, Mathematica notebooks are the ideal medium for all of your technical
projects. They are the main interface to all Mathematica computations and let you combine all of your
calculations, code, results, and graphics into one interactive technical document.
Notebooks are platform independent and combine interactive typeset Mathematical expressions, formatted
text, hyperlinks, graphics, animations, sound, and fully customizable buttons and palettes.
Mathematica's user interface includes such word-processing capabilities as spell checking (with a
large technical vocabulary) and automatic hyphenation.
You can send notebooks by email or put them on a website or an FTP site without affecting their
quality, use them to create high-quality printouts or sophisticated on-screen presentations, or
translate them to other document formats such as HTML, TeX, and MathML, part of the new XML standard.
Complex Analysis
High-speed numerics and high-level commands make complex analysis quick and easy.
Mathematica comes with a wide range of high-level statistics and data analysis functions as well as
powerful import, export, and connectivity functionality, making even complex analysis of large data
sets quick and easy. Mathematica's record-breaking speed for numerical linear algebra also makes
processing large data sets faster than ever.
Mathematica includes import and export filters for over 70 popular file formats, including XML.
Mathematica can also connect to databases with JDBC or .NET mechanisms through J/Link and
.NET/Link. Mathematica's connection tools also allow you to easily build and access online
data feeds, other data acquisition software such as LabView, and web services.
Once you have read your data files into Mathematica, you can apply sophisticated analysis or
visualization techniques or use Mathematica's computational power to build complex models.
Mathematica comes with fast tools for data manipulation, descriptive statistics of uni- and
multivariate data, generalized linear and nonlinear fitting, multidimensional interpolation,
convolution, correlation, regression, ANOVA, hypothesis testing, and visualization and statistical
plotting tools.
Additional packages for specialized analysis including time series, digital processing, neural
networks, and signal processing are available from Wolfram Research as well as independent developers.
Volumes of Knowledge
Put the world's largest collection of Mathematical knowledge at your fingertips.
Mathematica takes the most extensive collection of computation and visualization tools you'll find
anywhere and puts them right on your desktop. Mathematica contains and surpasses the knowledge of
thousands of Mathematical tables, hundreds of reference books, and dozens of software systems. Yet
Mathematica is faster to use, more accurate, and better integrated than any of them. All of the
components you need to pursue a solution are built into Mathematica, from the basic functions like
Sin, Log, and Eigenvalues to powerful
superfunctions such as Solve, Integrate, and Simplify.
Plotting Functions and Visualization
Mathematica provides many flexible plotting options for visualizing your results:
Plot,
Plot3D, ContourPlot,
DensityPlot, ArrayPlot,
ParametricPlot, MoviePlot,
MoviePlot3D,
LogPlot, LogLogPlot,
PolarPlot, ImplicitPlot,
ListPlot, ScatterPlot3D, and many other variations. Yet these
plotting routines represent only a subset of Mathematica's extensive graphics and visualization
capabilities.
Automatic Numeric-Precision Control
Mathematica keeps track of the precision of its numerical results automatically throughout each
calculation and adjusts its internal algorithms as needed to provide the precision you require.
Typesetting
Fully typeset input and output are interactive.
In addition to working with pure-text input and output, Mathematica works with typeset expressions.
Both text and Mathematical expressions can be formatted in any typeface, size, or style. Mathematical
expressions are also "live," and you can use them as input or can make instant modifications. This
feature allows you to work with Mathematical expressions that are familiar from textbooks and to
input formulas and parse results far more quickly than you can in any other program.
Symbolic and Numeric Computations
Perform symbolic as well as numeric computations.
Every function in Mathematica is implemented as completely as possible, handling the widest range of
numeric and symbolic inputs. Mathematica knows how to evaluate functions to any precision anywhere in
the complex plane. Along with supporting numerical inputs, Mathematica supports the world's largest
collection of symbolic transformation rules, allowing sophisticated manipulation and reduction of
formulas.
Pass the function Sin an exact input such as
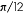 , and
the result comes back exactly as , and
the result comes back exactly as
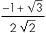 .
Pass it the numerical approximation 0.261799, and it returns the numerical result 0.258819. Try a
complex value, and you get a complex result. Since all of these cases are handled simply by calling
the function Sin, you won't need to memorize a different function name for each kind of argument. .
Pass it the numerical approximation 0.261799, and it returns the numerical result 0.258819. Try a
complex value, and you get a complex result. Since all of these cases are handled simply by calling
the function Sin, you won't need to memorize a different function name for each kind of argument.
Graphics
Choose from over 50 styles of graphics, or create your own.
Mathematica provides over 50 built-in graphics types for visualizing your results, including a variety
of 2D and 3D plots, contour and density graphics, and a full complement of specialized business and
statistical plots. Mathematica also lets you generate animations and sounds with simple commands.
However, these plotting routines represent only a subset of Mathematica's extensive graphics and
visualization capabilities. Mathematica also comes with a graphics language that lets you customize
graphics to your exact specifications or even create your own graphic types from a large set of
built-in primitives.
Application Development
Develop applications with Mathematica.
In many cases you want not only to publish your results but also to make your Mathematica applications
available to others--coworkers in your organization, customers, or colleagues around the world.
Mathematica's combination of computational sophistication and programmability makes it ideal for
prototyping and developing complete applications. Because it provides a high-level environment, you
can concentrate on what's unique to your work instead of spend time coding generic, low-level
functionality. Once your application is finished, Mathematica offers numerous ways to rapidly deploy
it in the way that is most efficient for your purpose.
Mathematica Notebooks and Packages
The most direct way of allowing others to use your Mathematica programs is to send your notebooks or
packages to them. All Mathematica documents and programs are fully platform independent, so you do not
have to worry about portability issues or incompatibilities. You can even add a point-and-click user
interface, using either Mathematica buttons and palettes or Java, so that end users never have to work
with the command line.
Interactive Web and Intranet Sites
With very little effort almost any Mathematica program can be turned into an MSP, an interactive web
application running on a webMathematica server. In many cases, the process requires only a few
steps--for example, saving the notebook as HTML, extracting the code, and then adding a few simple
Mathlet tags. The resulting web application can be used from any web browser and through an interface;
no Mathematica knowledge is required. You can also easily create more-advanced user interfaces using
any number of standard web-development tools and languages such as JavaScript, JSP, or PHP.
Mathematica as a Software Component
With Mathematica's J/Link and MathLink API, you can also deploy your Mathematica
application as part of a Java, .NET, or C/C++ program right out of the box. Additional products from
Wolfram Research and independent developers provide prebuilt links to Visual Basic, scripting
languages, and Microsoft Excel, which enable the products to interface with Mathematica and a variety
of application packages.
Programmable Palettes
Programmable palettes let you have instant access to sophisticated functionality.
Mathematica comes with a collection of ready-to-use palettes that give you instant access to many of
the built-in functions with one click. Because Mathematica is so flexible, you can also easily create
your own palettes in seconds.
Put the functions and symbols you use most often on a single palette, or make notebooks interactive by
including custom buttons in them. You can even add the palettes you use most often to a menu for
quick access or can send them via email to your colleagues.
Since you can run any Mathematica function or program from a button, you can build complete interfaces
to your Mathematica packages or courseware--making Mathematica an even more productive environment in
which to work.
Special-Purpose Interfaces
Create special-purpose interfaces using Java, .NET, or C/C++.
Mathematica allows you to create complete document-centric and graphical user interfaces. You can build
buttons and palettes, input forms and dialogs, and even fully interactive documents using nothing but
built-in Mathematica functions. Moreover, your programs can generate any of these interface elements
on the fly.
Automatically generate reports with completely cross-referenced hyperlinks. Create a survey that
adapts itself to the answers given by the user. Make self-modifying palettes. The possibilities are
endless, and the programs and interfaces created are platform independent.
There are many additional ways to generate custom user and programmatic interfaces for Mathematica. For
example, Mathematica now comes with J/Link and a Java Runtime Environment preinstalled, allowing you
to use AWT or Swing components to create a Java-based graphical user interface to Mathematica that
will run seamlessly on all platforms for which Mathematica and Java are available.
The Windows version of Mathematica also includes .NET/Link for full integration with the
Microsoft .NET Framework. With .NET/Link, Mathematica users can load any .NET object into
Mathematica and extend it. .NET/Link also provides an easy way to call any DLL or COM object
from within Mathematica.
Programming Language
Program in the uniquely productive Mathematica language.
Whether you call them simulations, models, or algorithms, representing your concepts in Mathematica is
easy. There's hardly a distinction between interactive and programmed calculations in Mathematica. You
can build intricate calculations piece by piece. Specify a definition for an expression. Look up a
formula and add it as a Mathematica transformation rule. Add more rules for other cases or for related
formulas. The intuitive nature of Mathematica lets you build surprisingly sophisticated calculations
easily and incrementally.
Mathematica includes a modern, wide-ranging, and highly versatile language that doesn't force you into
a single style of programming. Just as a spoken language gives you many ways to express each idea,
Mathematica provides many different programming paradigms.
Your code reflects your style of specifying the problem, which can make the command much shorter and
easier to read. This unique flexibility makes switching to Mathematica from other programming languages
easy--and cost effective. Even those who haven't programmed before can write powerful programs without
extensive training.
Concentrate on your ideas.
Mathematica takes care of the programming infrastructure. There is no need to predeclare variable
types or dimensions of lists and arrays, to direct memory management, or to compile your programs.
Common procedures such as sorting, searching, handling files, and manipulating data are built in and
remove peripheral code from your routines. This feature helps to make typical Mathematica programs
only 5 to 10 percent the size of those created in traditional languages or numerical systems and
greatly shrinks development time.
Choose your programming style.
Mathematica handles problems of any scale and complexity equally well; it's more than a simple
scripting language. One key feature is dynamic arrays of arbitrary size and dimension; optional
compilation is another. By providing multiple paradigms and the world's most powerful pattern-matching
engine, Mathematica lets you choose the most effective programming style for your problem. You don't
have to work around the limitations of a restrictive language.
With such a variety of programming approaches, it's easy to see why Mathematica has become the
language of choice for technical professionals around the world. Add it all together: Mathematica
makes you many times more productive.
Interactive Help Browser
All documentation is available through the interactive Help Browser.
The Mathematica Help Browser includes the complete documentation for all functions in Mathematica and
the entire text of The Mathematica Book as fully indexed Mathematica notebooks with advanced search
capabilities and comprehensive hyperlinks.
The Help Browser also contains thousands of interactive examples that demonstrate the use of
Mathematica functions, its general capabilities, and the best way to take advantage of them.
Modify and evaluate examples in the Help Browser.
Unlike any other software, Mathematica enables users to modify and evaluate expressions directly
within the Help Browser. The online material for the majority of built-in functions includes several
examples to be evaluated or altered, providing a particularly helpful aid for those who learn best by
example. User modifications of material within the Help Browser are not permanent, however. If you
accidentally delete an example or section of help text, you need only to exit and reenter that page
to restore the original information.
However, the material presented in the Help Browser is not fixed permanently to include only what is
provided with the Mathematica installation. Help Browser information is stored as a Mathematica
notebook. Thus, you can create help notebooks that become fully integrated with other Help Browser
information, including the insertion of new entries into the Help Browser's master index.
What's New in Mathematica 5.2
64-Bit Computing
Across all major platforms, Mathematica now supports 64-bit memory addressing and 64-bit long number
partitioning--both industry firsts that reflect Wolfram Research's commitment to delivering rapid
support for the latest computing technology.
Traditionally, operating systems have been 32-bit: able only to provide unique addresses for less than
232 bytes, or about 4.3GB of memory. Instead, Linux and new
operating system releases from Microsoft and Apple utilize 64-bit addressing--making
the memory limit 264 bytes, or about
18,000,000,000GB, although current hardware will only support a lower limit such as
242.
With Version 5.2, Mathematica is now the ideal platform for solving large problems on all major
operating systems:
- Its 64-bit support means that there's effectively no memory barrier.
- Long numbers are now broken into 64-bit rather than 32-bit lengths for processing, enabling better performance.
- Sparse and packed array technology introduced in Mathematica 4, 5.0, and 5.1 made computations highly memory efficient.
- Computational speed-ups beginning with Mathematica 5 have improved some calculation times as much as 1000-fold.
- Optional grid versions of Mathematica are available to distribute computations in parallel over multiple processors or computers.
At installation, Mathematica automatically detects whether to install the 32-bit or 64-bit version.
The images represent the snapshots of a tsunami as it passes over undersea mountains. The left image was computed with
near-maximum memory usage on a 32-bit memory system. The right image used the higher resolution that 64-bit computation
enables and avoided artifacts present in the 32-bit image.
Note that manipulating, analyzing, and visualizing data typically consumes significantly more memory than just the size
of the data itself, and that therefore 64-bit capability is often important even with data many times smaller than 4.3GB.
Vectorization
Major speed-ups have been attained on key platforms when applying elementary functions to vectors, matrices, and arrays of
floating-point numbers.
Packed array technology--introduced in Mathematica 4--achieves this by utilizing vectorized math libraries optimized for each
CPU. On certain platforms these libraries use multicore technology.
Secure Shell
Mathematica's computational kernel can be run on a computer that is separate from the user and front-end notebook interface.
This is advantageous in cases where a more-powerful remote computer is available.
Newly in Version 5.2, Mathematica can now communicate through a secure shell environment that is typical in many
organizations, rather than just insecure connections such as remote shell.
Multicore Support
Mathematica 5.2 introduces new support for threading of numerical linear algebra over multiple-CPU or multicore computers.
In addition, Mathematica's notebook front end is a separate process from its computational kernel, allowing them to run on
separate cores or CPUs. This gives a responsive interface even when the kernel core is under full load.
Multicore chips have more than one CPU core; multiple-processor computers have more than one CPU chip. Both are being introduced
by manufacturers to speed up tasks by splitting threads or processes among different processors so that they can be performed in
parallel.
Optional gridMathematica is available for tying together multiple computers, each containing one or several CPUs and/or cores.
Desktop Search
The Wolfram Notebook Indexer has been included with Mathematica 5.2.
After autoinstalling the correct plug-in for Google Desktop Search, Apple Spotlight, or Windows Desktop Search, the Indexer parses
notebook expressions so that Mathematica expressions, control language, arbitrary defined Unicode characters including Japanese,
Chinese, and other 16-bit characters can be searched for.
The Indexer supports extra features in certain search engines, such as special category identifiers in Spotlight.
Additional New Features in Version 5.2
- Enhancements to high-level special functions, including singularity handling, series expansion of algebraic
functions, and derivatives
- New algorithms for symbolic differential equations improve solvability of higher-order linear differential equations
- Enhanced performance for linear Diophantine systems
- Enhanced quadratic quantifier elimination improves symbolic solving capabilities
- Import now supports vCard contact information and RSS blog syndication filters
- MathematicaMark benchmark updated for Version 5.2, covering grids and clusters
- Stem and leaf statistics plots added
- And many more enhancements and innovations...
|
Mathematica for Windows
Platform Availability
| OperatingSystem |
Processor |
Version |
32/64-bit |
|
|
| | Windows XP x64 |
x86 (64-bit) |
5.2 |
64-bit |
| Windows Server 2003 x64 |
| Windows XP |
Pentium II class |
5.2 |
32-bit |
| Windows Server 2003 |
| Windows NT 4.0/2000 |
| Windows 98/Me |
The above content is Copyright © by Wolfram Research, Inc.
|
|
